11452. The longest path
Given a directed graph G with n
vertices and m edges. The vertices are numbered from 1 to n. For
each i (1 ≤ i ≤ m), a directed edge from
vertex xi to vertex уi is given.
The graph G contains no directed cycles.
Find the length of the longest directed
path in G. The length of a path is defined as the number of edges in that path.
Input. The first line contains two integers: the number of
vertices n (2 ≤ n ≤ 105) and the number of edges m (1 ≤ m ≤ 105) of the graph. Each of the next m
lines contains two integers xi, уi (1
≤ xi, уi ≤ n),
describing a directed edge from vertex xi to vertex уi.
Output. Print the length of the longest directed path in the
graph G.
|
Sample
input 1 |
Sample
output 1 |
|
4 5 1 2 1 3 3 2 2 4 3 4 |
3 |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
|
6 3 2 3 4 5 5 6 |
2 |
SOLUTION
graphs – topological sort
Algorithm analysis
Let’s
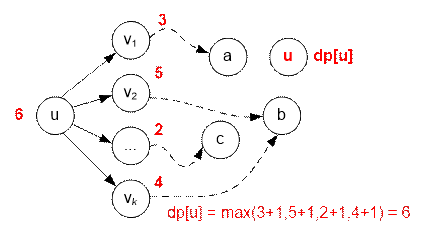
find a topological sort of the graph. Denote by dp[u]
the maximum number of cities that can be visited along a path starting from
vertex u.
Consider
the vertices in the order of the topological sort. Let u be the current
vertex. Let v1, v2, …, vk
be the vertices to which edges go from u. Then update the value as
follows:
dp[u] = max(dp[vi] + 1), 1 ≤ i ≤ k
Initially, set dp[u] = 0 (1
≤ u ≤ n).
After
processing all the vertices, find the greatest value in the dp array. It equals
the length of the longest path in the graph.
Example
On the left is the graph from the first example. On the right is the one
from the second example. The longest paths are highlighted.
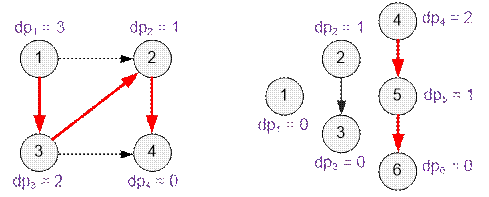
In the first example, the longest path equals dp1 = 3.
In the second example, the longest path equals dp4 = 2.
Algorithm implementation
Let’s
declare the adjacency list of the graph g.
vector<vector<int> > g;
The
function dfs performs a depth-first search starting from vertex v.
We topologically sort the vertices of the graph and store them in the array top.
void dfs(int v)
{
used[v] = 1;
for (int to : g[v])
if (used[to] == 0) dfs(to);
top.push_back(v);
}
The
main part of the program. Read the input data. Bild the adjacency list of the
directed graph.
scanf("%d %d", &n, &m);
g.resize(n
+ 1);
while (m--)
{
scanf("%d %d", &a, &b);
g[a].push_back(b);
}
Run
a depth-first search on the disconnected graph.
used.resize(n
+ 1);
for (i = 1; i <= n; i++)
if (used[i] == 0) dfs(i);
Iterate
over the vertices of the graph in the order opposite to their topological sort,
that is, we iterate over the vertices in the top array from left to
right.
dp.resize(n
+ 1);
for (int u : top)
{
A
path from vertex u to itself has length 0 (initialization).
dp[u] = 0;
Iterate
over the vertices v adjacent to u. Consider the edge (u, v).
for (int v : g[u])
For
all such vertices v, find the maximum among the values dp[v] +
1.
dp[u] = max(dp[u], dp[v] + 1);
}
Find
and print the largest element in the dp array. It corresponds to the
length of the longest path in the graph.
res = *max_element(dp.begin(), dp.end());
printf("%d\n", res);